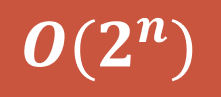Recursive (Özyinelemeli) Fonksiyon Analizi #1 Iteration Method (Tekrarlama Yöntemi)

Giriş
Öz yinelemeli fonksiyonlar kendi içerisinde tekrar tekrar kendisini çağıran fonksiyonlardır. Tam da bu yüzden bu algoritmaların analizini yapmak standart fonksiyonlara göre daha zahmetlidir.
Algoritma analizi kapsamında recursive olmayan fonksiyonların analizi standart yöntemlerle kolay bir şekilde gerçekleştirilebilirken recursive fonksiyonlarda işler biraz karışabiliyor. Bu fonksiyonların analizini gerçekleştirmek için birkaç yöntem bulunmaktadır. Bu yazıda bir özyinelemeli algoritmanın analiz analiz yöntemlerinden bahsederek Iteration Methodu ile Hanoi Kuleleri algoritmasının analizini gerçekleştireceğiz.
Temel olarak 2 adım ile bu fonksiyonların analizi gerçekleştirilebilir:
- Algoritmanın zamana bağlı denkleminin T(n) elde edilmesi.
- Elde edilen denklemin Substitution, Iterasyon, Recursion Tree veya Master yöntemleriyle çözülmesi.
Birinci adım için daha önce yazmış olduğum Recursive (Özyinelemeli) Fonksiyonlarda Zaman Denklemini Bulma yazımı okuyabilirsiniz.
Bu yazıda ikinci adım olan T(n)‘i bilinen bir algoritmanın Iteration teoremini kullanarak analizini gerçekleştireceğiz.
Iteration (İterasyon-Yineleme) Metodu
Iteration metodu, bir recursive denklemi çözmek için kullanılan tekniklerden biridir. T(n) denklemini ardışık adımlarla açarak, fonksiyonun kapalı formunu (closed form) elde etmeye çalışır. Bu yöntemin temel adımları şu şekilde sıralanabilir:
- T(n) denkleminin bulunması
- Bulunan T(n)’in tekrar tekrar açılması
- Genelleme yapılması, genel bir ifade bulunması
- Durdurma koşulunun hesaplanması
- Kapalı formun elde edilmesi
Şimdi bu adımları Hanoi Kuleleri algoritması üzerinde sırayla gerçekleştireceğiz. Analize geçmeden önce kısaca Hanoi Kuleleri algoritmasına değinebiliriz.
Hanoi Kuleleri Algoritması
Kısaca bir çubuk üzerindeki blokları diğer çubuğa en altta en büyük en üstte ise en küçük blok olacak şekilde taşınmasını hedefleyen algoritmadır ve aşağıdaki görsel ile anlatılabilir. Yalnız bu işlemi gerçekleştirmek için 2 kural bulunuyor. Her hamlede yalnızca 1 blok hareket ettirilebilir ve hiçbir hamlede küçük bir bloğun üstünde büyük bir blok olamaz.

Bu algoritmayı koda dökecek olursak aşağıdaki gibi bir recursive fonksiyon yazabiliriz. Blokları A çubuğundan C çubuğuna taşımak istiyoruz.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
package main func main() { hanoi(3, "A", "C", "B") } func hanoi(n int, from, to, aux string) { if n >= 1 { hanoi(n-1, from, aux, to) move(from, to) hanoi(n-1, aux, to, from) } } func move(from, to string) { println("Move disk from", from, "to", to) } |
Şimdi analiz adımlarına geçebiliriz.
1) T(n) denkleminin bulunması
Recursive fonksiyon çağırımlarının ikisi de n-1 kez çalışacaktır. Dolayısıyla ikisine de T(n-1) diyebiliriz. ortadaki move fonksiyonu ise herhangi bir recursive çağırım yapmadığı için O(1) diyebiliriz. Oluşan ifadeleri topladığımızda T(n) denklemini T(n)=2T(n-1)+1 şeklinde elde ederiz.

2) Bulunan T(n)’in Tekrar Tekrar Açılması
Denklemimizde O(1) yerine sabit olarak c yazabiliriz. Ardından n yerine birkaç kez fonksiyonun kendi değerini yazarak tekrar tekrar açtığımızda aşağıdaki gibi 8T(n-3)+7c ifadesini elde edeceğiz.
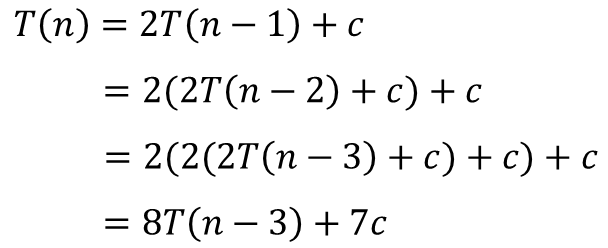
3) Genelleme yapılması, genel bir ifade bulunması
Elde ettiğimiz T(n)=8T(n-3)+7c ifadesini biraz düzenleyelim. 8 yerine 2^3 ve 7 yerine 2^3 – 1 yazabiliriz. İfademizin son hali şöyle olur:
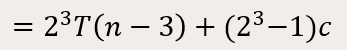
Fark edildiği üzere bu ifadede 3 sayısı ortak bir hale geldi. 3 yerine k yazalım. Şu ifadeyi elde ederiz:
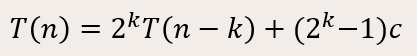
Böylelikle ifadeyi genelleştirerek değişkenli bir hale dönüştürdük. Sonraki adıma geçebiliriz.
4) Durdurma koşulunun hesaplanması
Durdurma koşulunun hesaplanması adımı ifadede T içerisini sıfıra eşitlemekten geçer. Yani n-k = 0 ifadesini çözmemiz gerekir. Sonuç olarak n=k elde ederiz. Durdurma koşulumuzu n olarak elde ettik.
5) Kapalı formun elde edilmesi
Son adımda ise bir önceki adıma bulduğumuz durdurma koşulunu denklemde k yerine yazmamız gerekiyor.
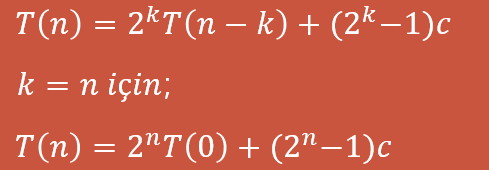
Eğer T(0)=0 ise;
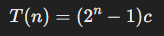
Sabitler asimptotik büyüme hızını etkilemeyeceğinden dolayı yaptığımız analiz sonucu algoritmanın çalışma süresi O(2^n) elde edilir.